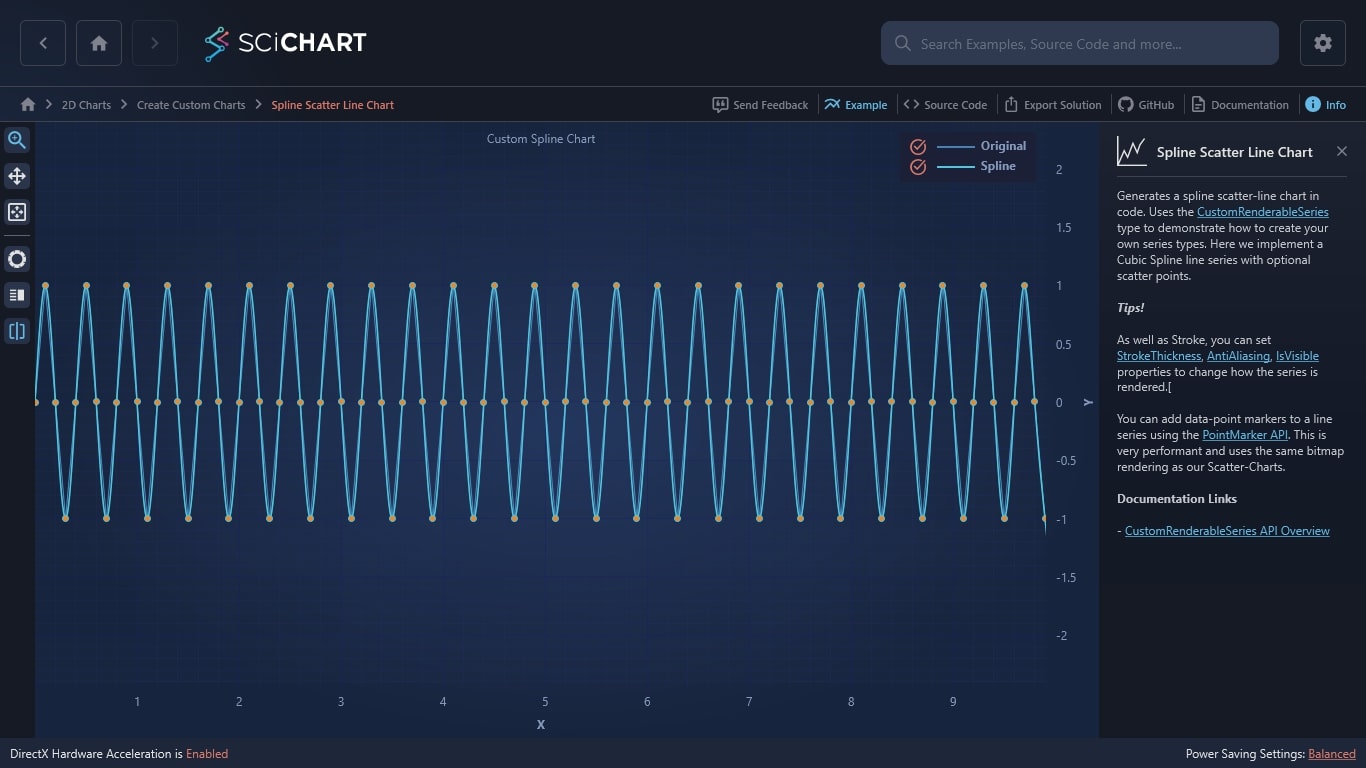
Generates a spline scatter-line chart in code. Uses the CustomRenderableSeries type to demonstrate how to create your own series types. Here we implement a Cubic Spline line series with optional scatter points.

Tips!

As well as Stroke, you can set StrokeThickness, AntiAliasing, IsVisible properties to change how the series is rendered.[

You can add data-point markers to a line series using the PointMarker API. This is very performant and uses the same bitmap rendering as our Scatter-Charts.

Documentation Links

• CustomRenderableSeries Type
• The RenderableSeries API
• The Immediate Mode RenderContext API

// SplineChartExampleView.xaml

<UserControl x:Class="SciChart.Examples.Examples.CreateACustomChart.SplineLineSeries.SplineChartExampleView"
             xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
             xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
             xmlns:s="http://schemas.abtsoftware.co.uk/scichart"
             xmlns:ext="http://schemas.abtsoftware.co.uk/scichart/exampleExternals"
             xmlns:local="clr-namespace:SciChart.Examples.Examples.CreateACustomChart.SplineLineSeries"
             Loaded="SplineChartExampleView_Loaded"
             xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006"
             xmlns:d="http://schemas.microsoft.com/expression/blend/2008"
             d:DesignHeight="400"
             d:DesignWidth="600"
             mc:Ignorable="d">

    <UserControl.Resources>

        <!-- The style for the rollover line -->
        <Style x:Key="RolloverLineStyle" TargetType="Line">
            <Setter Property="Stroke" Value="DarkGreen"/>
            <Setter Property="StrokeThickness" Value="2"/>
            <Setter Property="StrokeDashArray" Value="2 2"/>
            <Setter Property="IsHitTestVisible" Value="False"/>
            <Setter Property="UseLayoutRounding" Value="True"/>
        </Style>

    </UserControl.Resources>
    <Grid>

        <Grid.ColumnDefinitions>
            <ColumnDefinition Width="Auto" />
            <ColumnDefinition Width="*" />
        </Grid.ColumnDefinitions>

        <!--  The SciChartInteractionToolbar adds zoom, pan, zoom extents and rotate functionality  -->
        <!--  to the chart and is included for example purposes.  -->
        <!--  If you wish to know how to zoom and pan a chart then do a search for Zoom Pan in the Examples suite!  -->
        <ext:SciChartInteractionToolbar TargetSurface="{Binding Source={x:Reference Name=sciChart}}"/>
        
        <!--  Create the chart surface  -->
        <s:SciChartSurface Name="sciChart" Padding="0" BorderThickness="0" Grid.Column="1">

            <s:SciChartSurface.Annotations>
                <s:TextAnnotation Text="Custom Spline Chart" HorizontalAnchorPoint="Center" VerticalAnchorPoint="Top" X1="0.5" Y1="0.01" CoordinateMode="Relative"/>
            </s:SciChartSurface.Annotations>
            
            <!--  Declare RenderableSeries  -->
            <s:SciChartSurface.RenderableSeries>

                <!-- Draw the original line -->
                <s:FastLineRenderableSeries x:Name="LineRenderSeries" Stroke="SteelBlue" StrokeThickness="1" RolloverMarkerTemplate="{x:Null}" />

                <!-- Draw the spline series - custom renderable series -->
                <local:SplineLineRenderableSeries x:Name="SplineRenderSeries" Stroke="DarkGreen" StrokeThickness="2"  
                                                  IsSplineEnabled="True" UpSampleFactor="10">

                    <!-- LegendMarkerTemplate is required to show a marker in the legend next to SeriesName -->
                    <local:SplineLineRenderableSeries.LegendMarkerTemplate>
                        <DataTemplate>
                            <Line VerticalAlignment="Center" Stretch="Fill" Stroke="DarkGreen"
                                    StrokeThickness="2" X1="0" X2="1" Y1="0.5" Y2="0.5" />
                        </DataTemplate>
                    </local:SplineLineRenderableSeries.LegendMarkerTemplate>

                    <!-- PointMarker is optional, to display a marker on each data point -->
                    <local:SplineLineRenderableSeries.PointMarker>
                        <s:EllipsePointMarker Fill="White" Stroke="DarkGreen"/>
                    </local:SplineLineRenderableSeries.PointMarker>

                    <!-- RolloverMarker is optional, to display a marker on Rollover -->
                    <local:SplineLineRenderableSeries.RolloverMarkerTemplate>
                        <ControlTemplate>
                            <Ellipse Width="9" Height="9" Fill="White" Stroke="DarkGreen" StrokeThickness="1"></Ellipse>
                        </ControlTemplate>
                    </local:SplineLineRenderableSeries.RolloverMarkerTemplate>

                </local:SplineLineRenderableSeries>

            </s:SciChartSurface.RenderableSeries>

            <!--  Create an X Axis with Growby  -->
            <s:SciChartSurface.XAxis>
                <s:NumericAxis AxisTitle="X" TextFormatting="#.############" ScientificNotation="None" DrawMajorBands="True"/>
            </s:SciChartSurface.XAxis>

            <!--  Create a Y Axis with Growby. Optional bands give a cool look and feel for minimal performance impact  -->
            <s:SciChartSurface.YAxis>
                <s:NumericAxis AxisTitle="Y" GrowBy="0.7, 0.7" DrawMajorBands="True"/>
            </s:SciChartSurface.YAxis>

            <s:SciChartSurface.ChartModifier>
                <s:ModifierGroup>
                    <s:RubberBandXyZoomModifier x:Name="RubberBandXyZoomModifier" IsEnabled="True"/>
                    <s:ZoomPanModifier x:Name="ZoomPanModifier" IsEnabled="False" ClipModeX="None"/>
                    <s:LegendModifier ShowLegend="True" LegendPlacement="Inside" Margin="10" VerticalAlignment="Top" HorizontalAlignment="Right"/>
                    <s:RolloverModifier x:Name="RolloverModifier" ShowAxisLabels="False" 
                                        UseInterpolation="True"
                                        LineOverlayStyle="{StaticResource RolloverLineStyle}"
                                        ShowTooltipOn="Always"/>
                    <s:XAxisDragModifier/>
                    <s:YAxisDragModifier/>
                    <s:ZoomExtentsModifier/>
                </s:ModifierGroup>
            </s:SciChartSurface.ChartModifier>

        </s:SciChartSurface>

    </Grid>
</UserControl>

// SplineChartExampleView.xaml.cs

// *************************************************************************************
// SCICHART® Copyright SciChart Ltd. 2011-2018. All rights reserved.
//  
// Web: http://www.scichart.com
//   Support: support@scichart.com
//   Sales:   sales@scichart.com
// 
// SplineChartExampleView.xaml.cs is part of the SCICHART® Examples. Permission is hereby granted
// to modify, create derivative works, distribute and publish any part of this source
// code whether for commercial, private or personal use. 
// 
// The SCICHART® examples are distributed in the hope that they will be useful, but
// without any warranty. It is provided "AS IS" without warranty of any kind, either
// expressed or implied. 
// *************************************************************************************
using System.Windows;
using System.Windows.Controls;
using SciChart.Charting.Model.DataSeries;
using SciChart.Examples.ExternalDependencies.Data;

namespace SciChart.Examples.Examples.CreateACustomChart.SplineLineSeries
{
    /// <summary>
    /// Interaction logic for CustomChartExampleView.xaml
    /// </summary>
    public partial class SplineChartExampleView : UserControl
    {
        public SplineChartExampleView()
        {
            InitializeComponent();
        }

        private void SplineChartExampleView_Loaded(object sender, RoutedEventArgs e)
        {
            // Create a DataSeries of type X=double, Y=double
            var originalData = new XyDataSeries<double, double>() {SeriesName = "Original"};
            var splineData = new XyDataSeries<double, double>() { SeriesName = "Spline" };

            LineRenderSeries.DataSeries = originalData;
            SplineRenderSeries.DataSeries = splineData;

            var data = DataManager.Instance.GetSinewave(1.0, 0.0, 100, 25);

            // Append data to series. SciChart automatically redraws
            originalData.Append(data.XData, data.YData);
            splineData.Append(data.XData, data.YData);

            sciChart.ZoomExtents();
        }
    }
}

// SplineLineRenderableSeries.cs

// *************************************************************************************
// SCICHART® Copyright SciChart Ltd. 2011-2018. All rights reserved.
//  
// Web: http://www.scichart.com
//   Support: support@scichart.com
//   Sales:   sales@scichart.com
// 
// SplineLineRenderableSeries.cs is part of the SCICHART® Examples. Permission is hereby granted
// to modify, create derivative works, distribute and publish any part of this source
// code whether for commercial, private or personal use. 
// 
// The SCICHART® examples are distributed in the hope that they will be useful, but
// without any warranty. It is provided "AS IS" without warranty of any kind, either
// expressed or implied. 
// *************************************************************************************
using System;
using System.Collections.Generic;
using System.Linq;
using System.Windows;
using SciChart.Charting.Visuals.RenderableSeries;
using SciChart.Data.Model;
using SciChart.Drawing.Common;

namespace SciChart.Examples.Examples.CreateACustomChart.SplineLineSeries
{
    /// <summary>
    /// A CustomRenderableSeries example which uses a Cubic Spline algorithm to smooth the points in a FastLineRenderableSeries
    /// </summary>
    public class SplineLineRenderableSeries : CustomRenderableSeries
    {
        public static readonly DependencyProperty IsSplineEnabledProperty =
            DependencyProperty.Register("IsSplineEnabled", typeof (bool), typeof (SplineLineRenderableSeries),
                new PropertyMetadata(default(bool)));

        public bool IsSplineEnabled
        {
            get { return (bool) GetValue(IsSplineEnabledProperty); }
            set { SetValue(IsSplineEnabledProperty, value); }
        }

        public static readonly DependencyProperty UpSampleFactorProperty = DependencyProperty.Register(
            "UpSampleFactor", typeof (int), typeof (SplineLineRenderableSeries), new PropertyMetadata(10));

        public int UpSampleFactor
        {
            get { return (int) GetValue(UpSampleFactorProperty); }
            set { SetValue(UpSampleFactorProperty, value); }
        }

        private IList<Point> _splineSeries;

        /// <summary>
        /// Draws the series using the <see cref="IRenderContext2D" /> and the <see cref="IRenderPassData" /> passed in
        /// </summary>
        /// <param name="renderContext">The render context. This is a graphics object which has methods to draw lines, quads and polygons to the screen</param>
        /// <param name="renderPassData">The render pass data. Contains a resampled 
        /// <see cref="IPointSeries" />, the 
        /// <see cref="IndexRange" /> of points on the screen
        /// and the current YAxis and XAxis 
        /// <see cref="ICoordinateCalculator{T}" /> to convert data-points to screen points</param>
        protected override void Draw(IRenderContext2D renderContext, IRenderPassData renderPassData)
        {
            base.Draw(renderContext, renderPassData);

            // Get the data from RenderPassData. See CustomRenderableSeries article which describes PointSeries relationship to DataSeries
            if (renderPassData.PointSeries.Count == 0) return;

            // Convert to Spline Series
            _splineSeries = ComputeSplineSeries(renderPassData.PointSeries, IsSplineEnabled, UpSampleFactor);

            // Get the coordinates of the first dataPoint
            var point = GetCoordinatesFor(_splineSeries[0].X, _splineSeries[0].Y);

            // Create a pen to draw the spline line. Make sure you dispose it!             
            using (var linePen = renderContext.CreatePen(this.Stroke, this.AntiAliasing, this.StrokeThickness))
            {
                // Create a line drawing context. Make sure you dispose it!
                // NOTE: You can create mutliple line drawing contexts to draw segments if you want
                //       You can also call renderContext.DrawLine() and renderContext.DrawLines(), but the lineDrawingContext is higher performance
                using (var lineDrawingContext = renderContext.BeginLine(linePen, point.X, point.Y))
                {
                    for (int i = 1; i < _splineSeries.Count; i++)
                    {
                        point = GetCoordinatesFor(_splineSeries[i].X, _splineSeries[i].Y);

                        lineDrawingContext.MoveTo(point.X, point.Y);
                    }
                }
            }

            DrawPointMarkers(renderContext, renderPassData.PointSeries);
        }

        private Point GetCoordinatesFor(double xValue, double yValue)
        {
            // Get the coordinateCalculators. See 'Converting Pixel Coordinates to Data Coordinates' documentation for coordinate transforms
            var xCoord = CurrentRenderPassData.XCoordinateCalculator.GetCoordinate(xValue);
            var yCoord = CurrentRenderPassData.YCoordinateCalculator.GetCoordinate(yValue);

            if (CurrentRenderPassData.IsVerticalChart)
            {
                Swap(ref xCoord, ref yCoord);
            }
            
            return new Point(xCoord, yCoord);
        }

        private void Swap(ref double arg1, ref double arg2)
        {
            var tmp = arg2;

            arg2 = arg1;
            arg1 = tmp;
        }

        public override HitTestInfo HitTest(Point rawPoint, double hitTestRadius, bool interpolate = false)
        {
            var nearestBaseHitResult = base.HitTest(rawPoint, hitTestRadius, interpolate);
            
            // No spline? Fine - return base implementation
            if (!IsSplineEnabled || _splineSeries == null || CurrentRenderPassData == null)
                return nearestBaseHitResult;

            var nearestHitResult = new HitTestInfo();

            // Get the coordinateCalculators. See 'Converting Pixel Coordinates to Data Coordinates' documentation for coordinate transforms
            var xCalc = CurrentRenderPassData.XCoordinateCalculator;
            
            // Compute the X,Y data value at the mouse location
            var xDataPointAtMouse = xCalc.GetDataValue(CurrentRenderPassData.IsVerticalChart ? rawPoint.Y : rawPoint.X);

            // Find the index in the spline interpolated data that is nearest to the X-Data point at mouse
            // NOTE: This assumes the data is sorted in ascending direction and a binary search would be faster ... 
            int foundIndex = FindIndex(_splineSeries, xDataPointAtMouse);

            if (foundIndex != -1)
            {
                nearestHitResult.IsWithinDataBounds = true;

                // Find the nearest data point to the mouse 
                var xDataPointNearest = _splineSeries[foundIndex].X;
                var yDataPointNearest = _splineSeries[foundIndex].Y;
                nearestHitResult.XValue = xDataPointNearest;
                nearestHitResult.YValue = yDataPointNearest;

                // Compute the X,Y coordinates (pixel coords) of the nearest data point to the mouse
                nearestHitResult.HitTestPoint = nearestHitResult.HitTestPoint = GetCoordinatesFor(xDataPointNearest, yDataPointNearest);
                
                // Determine if mouse-location is within 7.07 pixels of the nearest data point
                var distance = Math.Pow(rawPoint.X - nearestHitResult.HitTestPoint.X, 2) +
                               Math.Pow(rawPoint.Y - nearestHitResult.HitTestPoint.Y, 2);
                distance = Math.Sqrt(distance);
                
                var baseDistance = Math.Pow(rawPoint.X - nearestBaseHitResult.HitTestPoint.X, 2) + 
                                   Math.Pow(rawPoint.Y - nearestBaseHitResult.HitTestPoint.Y, 2);
                baseDistance = Math.Sqrt(baseDistance);

                nearestHitResult.IsHit = distance <= DefaultHitTestRadius || baseDistance <= DefaultHitTestRadius;
                nearestHitResult.IsVerticalHit = true;
                nearestHitResult.DataSeriesIndex = nearestBaseHitResult.DataSeriesIndex;

                if (DataSeries.HasMetadata)
                    nearestHitResult.Metadata = DataSeries.Metadata[nearestHitResult.DataSeriesIndex];

                // Returning a HitTestResult with IsHit = true / IsVerticalHit signifies to the Rollovermodifier & TooltipModifier to show a tooltip at this location
                return nearestHitResult;
            }
            else
            {
                // Returning HitTestInfo.Empty signifies to the RolloverModifier & TooltipModifier there is nothing to show here
                return HitTestInfo.Empty;
            }
        }
        
        // Cubic Spline interpolation: http://www.codeproject.com/Articles/560163/Csharp-Cubic-Spline-Interpolation
        private IList<Point> ComputeSplineSeries(IPointSeries inputPointSeries, bool isSplineEnabled, int upsampleBy)
        {
            IList<Point> result = null;

            if (!isSplineEnabled)
            {
                // No spline, just return points. Note: for large datasets, even the copy here causes performance problems!                 
                result = new List<Point>(inputPointSeries.Count);
                for (int i = 0; i < inputPointSeries.Count; i++)
                {
                    result.Add(new Point(inputPointSeries.XValues[i], inputPointSeries.YValues[i]));
                }
                return result;
            }

            // Spline enabled
            int n = inputPointSeries.Count * upsampleBy;
            var x = inputPointSeries.XValues.ToArray();
            var y = inputPointSeries.YValues.ToArray();
            double[] xs = new double[n];
            double stepSize = (x[x.Length - 1] - x[0]) / (n - upsampleBy);

            for (int i = 0; i < n; i++)
            {
                xs[i] = x[0] + i * stepSize;
            }

            var cubicSpline = new CubicSpline();
            double[] ys = cubicSpline.FitAndEval(x, y, xs);

            result = new List<Point>(n);
            for (int i = 0; i < xs.Length; i++)
            {
                result.Add(new Point(xs[i], ys[i]));
            }
            return result;
        }

        private int FindIndex(IList<Point> list, double value)
        {
            for (int i = 0; i < list.Count; i++)
            {
                if (list[i].X.CompareTo(value) >= 0)
                    return i;
            }

            return -1;
        }
    }
}

// CubicSpline.cs

// *************************************************************************************
// SCICHART® Copyright SciChart Ltd. 2011-2018. All rights reserved.
//  
// Web: http://www.scichart.com
//   Support: support@scichart.com
//   Sales:   sales@scichart.com
// 
// CubicSpline.cs is part of the SCICHART® Examples. Permission is hereby granted
// to modify, create derivative works, distribute and publish any part of this source
// code whether for commercial, private or personal use. 
// 
// The SCICHART® examples are distributed in the hope that they will be useful, but
// without any warranty. It is provided "AS IS" without warranty of any kind, either
// expressed or implied. 
// *************************************************************************************
using System;

namespace SciChart.Examples.Examples.CreateACustomChart.SplineLineSeries
{
    /// <summary>
    /// Cubic spline interpolation.
    /// Call Fit (or use the corrector constructor) to compute spline coefficients, then Eval to evaluate the spline at other X coordinates.
    /// </summary>
    /// <remarks>
    /// <para>
    /// This is implemented based on the wikipedia article:
    /// http://en.wikipedia.org/wiki/Spline_interpolation
    /// I'm not sure I have the right to include a copy of the article so the equation numbers referenced in 
    /// comments will end up being wrong at some point.
    /// </para>
    /// <para>
    /// This is not optimized, and is not MT safe.
    /// This can extrapolate off the ends of the splines.
    /// You must provide points in X sort order.
    /// </para>
    /// </remarks>
    public class CubicSpline
    {
        #region Fields

        // N-1 spline coefficients for N points
        private double[] a;
        private double[] b;

        // Save the original x and y for Eval
        private double[] xOrig;
        private double[] yOrig;

        #endregion

        #region Ctor

        /// <summary>
        /// Default ctor.
        /// </summary>
        public CubicSpline()
        {
        }

        /// <summary>
        /// Construct and call Fit.
        /// </summary>
        /// <param name="x">Input. X coordinates to fit.</param>
        /// <param name="y">Input. Y coordinates to fit.</param>
        /// <param name="startSlope">Optional slope constraint for the first point. Single.NaN means no constraint.</param>
        /// <param name="endSlope">Optional slope constraint for the final point. Single.NaN means no constraint.</param>
        /// <param name="debug">Turn on console output. Default is false.</param>
        public CubicSpline(double[] x, double[] y, double startSlope = double.NaN, double endSlope = double.NaN, bool debug = false)
        {
            Fit(x, y, startSlope, endSlope, debug);
        }

        #endregion

        #region Private Methods

        /// <summary>
        /// Throws if Fit has not been called.
        /// </summary>
        private void CheckAlreadyFitted()
        {
            if (a == null) throw new Exception("Fit must be called before you can evaluate.");
        }

        private int _lastIndex = 0;

        /// <summary>
        /// Find where in xOrig the specified x falls, by simultaneous traverse.
        /// This allows xs to be less than x[0] and/or greater than x[n-1]. So allows extrapolation.
        /// This keeps state, so requires that x be sorted and xs called in ascending order, and is not multi-thread safe.
        /// </summary>
        private int GetNextXIndex(double x)
        {
            if (x < xOrig[_lastIndex])
            {
                throw new ArgumentException("The X values to evaluate must be sorted.");
            }

            while ((_lastIndex < xOrig.Length - 2) && (x > xOrig[_lastIndex + 1]))
            {
                _lastIndex++;
            }

            return _lastIndex;
        }

        /// <summary>
        /// Evaluate the specified x value using the specified spline.
        /// </summary>
        /// <param name="x">The x value.</param>
        /// <param name="j">Which spline to use.</param>
        /// <param name="debug">Turn on console output. Default is false.</param>
        /// <returns>The y value.</returns>
        private double EvalSpline(double x, int j, bool debug = false)
        {
            double dx = xOrig[j + 1] - xOrig[j];
            double t = (x - xOrig[j]) / dx;
            double y = (1 - t) * yOrig[j] + t * yOrig[j + 1] + t * (1 - t) * (a[j] * (1 - t) + b[j] * t); // equation 9
            if (debug) Console.WriteLine("xs = {0}, j = {1}, t = {2}", x, j, t);
            return y;
        }

        #endregion

        #region Fit*

        /// <summary>
        /// Fit x,y and then eval at points xs and return the corresponding y's.
        /// This does the "natural spline" style for ends.
        /// This can extrapolate off the ends of the splines.
        /// You must provide points in X sort order.
        /// </summary>
        /// <param name="x">Input. X coordinates to fit.</param>
        /// <param name="y">Input. Y coordinates to fit.</param>
        /// <param name="xs">Input. X coordinates to evaluate the fitted curve at.</param>
        /// <param name="startSlope">Optional slope constraint for the first point. Single.NaN means no constraint.</param>
        /// <param name="endSlope">Optional slope constraint for the final point. Single.NaN means no constraint.</param>
        /// <param name="debug">Turn on console output. Default is false.</param>
        /// <returns>The computed y values for each xs.</returns>
        public double[] FitAndEval(double[] x, double[] y, double[] xs, double startSlope = double.NaN, double endSlope = double.NaN, bool debug = false)
        {
            Fit(x, y, startSlope, endSlope, debug);
            return Eval(xs, debug);
        }

        /// <summary>
        /// Compute spline coefficients for the specified x,y points.
        /// This does the "natural spline" style for ends.
        /// This can extrapolate off the ends of the splines.
        /// You must provide points in X sort order.
        /// </summary>
        /// <param name="x">Input. X coordinates to fit.</param>
        /// <param name="y">Input. Y coordinates to fit.</param>
        /// <param name="startSlope">Optional slope constraint for the first point. Single.NaN means no constraint.</param>
        /// <param name="endSlope">Optional slope constraint for the final point. Single.NaN means no constraint.</param>
        /// <param name="debug">Turn on console output. Default is false.</param>
        public void Fit(double[] x, double[] y, double startSlope = double.NaN, double endSlope = double.NaN, bool debug = false)
        {
            if (Double.IsInfinity(startSlope) || Double.IsInfinity(endSlope))
            {
                throw new Exception("startSlope and endSlope cannot be infinity.");
            }

            // Save x and y for eval
            this.xOrig = x;
            this.yOrig = y;

            int n = x.Length;
            double[] r = new double[n]; // the right hand side numbers: wikipedia page overloads b

            TriDiagonalMatrixF m = new TriDiagonalMatrixF(n);
            double dx1, dx2, dy1, dy2;

            // First row is different (equation 16 from the article)
            if (double.IsNaN(startSlope))
            {
                dx1 = x[1] - x[0];
                m.C[0] = 1.0f / dx1;
                m.B[0] = 2.0f * m.C[0];
                r[0] = 3 * (y[1] - y[0]) / (dx1 * dx1);
            }
            else
            {
                m.B[0] = 1;
                r[0] = startSlope;
            }

            // Body rows (equation 15 from the article)
            for (int i = 1; i < n - 1; i++)
            {
                dx1 = x[i] - x[i - 1];
                dx2 = x[i + 1] - x[i];

                m.A[i] = 1.0f / dx1;
                m.C[i] = 1.0f / dx2;
                m.B[i] = 2.0f * (m.A[i] + m.C[i]);

                dy1 = y[i] - y[i - 1];
                dy2 = y[i + 1] - y[i];
                r[i] = 3 * (dy1 / (dx1 * dx1) + dy2 / (dx2 * dx2));
            }

            // Last row also different (equation 17 from the article)
            if (double.IsNaN(endSlope))
            {
                dx1 = x[n - 1] - x[n - 2];
                dy1 = y[n - 1] - y[n - 2];
                m.A[n - 1] = 1.0f / dx1;
                m.B[n - 1] = 2.0f * m.A[n - 1];
                r[n - 1] = 3 * (dy1 / (dx1 * dx1));
            }
            else
            {
                m.B[n - 1] = 1;
                r[n - 1] = endSlope;
            }

//            if (debug) Console.WriteLine("Tri-diagonal matrix:\n{0}", m.ToDisplayString(":0.0000", "  "));
//            if (debug) Console.WriteLine("r: {0}", ArrayUtil.ToString<double>(r));

            // k is the solution to the matrix
            double[] k = m.Solve(r);
//            if (debug) Console.WriteLine("k = {0}", ArrayUtil.ToString<double>(k));

            // a and b are each spline's coefficients
            this.a = new double[n - 1];
            this.b = new double[n - 1];

            for (int i = 1; i < n; i++)
            {
                dx1 = x[i] - x[i - 1];
                dy1 = y[i] - y[i - 1];
                a[i - 1] = k[i - 1] * dx1 - dy1; // equation 10 from the article
                b[i - 1] = -k[i] * dx1 + dy1; // equation 11 from the article
            }

//            if (debug) Console.WriteLine("a: {0}", ArrayUtil.ToString<double>(a));
//            if (debug) Console.WriteLine("b: {0}", ArrayUtil.ToString<double>(b));
        }

        #endregion

        #region Eval*

        /// <summary>
        /// Evaluate the spline at the specified x coordinates.
        /// This can extrapolate off the ends of the splines.
        /// You must provide X's in ascending order.
        /// The spline must already be computed before calling this, meaning you must have already called Fit() or FitAndEval().
        /// </summary>
        /// <param name="x">Input. X coordinates to evaluate the fitted curve at.</param>
        /// <param name="debug">Turn on console output. Default is false.</param>
        /// <returns>The computed y values for each x.</returns>
        public double[] Eval(double[] x, bool debug = false)
        {
            CheckAlreadyFitted();

            int n = x.Length;
            double[] y = new double[n];
            _lastIndex = 0; // Reset simultaneous traversal in case there are multiple calls

            for (int i = 0; i < n; i++)
            {
                // Find which spline can be used to compute this x (by simultaneous traverse)
                int j = GetNextXIndex(x[i]);

                // Evaluate using j'th spline
                y[i] = EvalSpline(x[i], j, debug);
            }

            return y;
        }

        /// <summary>
        /// Evaluate (compute) the slope of the spline at the specified x coordinates.
        /// This can extrapolate off the ends of the splines.
        /// You must provide X's in ascending order.
        /// The spline must already be computed before calling this, meaning you must have already called Fit() or FitAndEval().
        /// </summary>
        /// <param name="x">Input. X coordinates to evaluate the fitted curve at.</param>
        /// <param name="debug">Turn on console output. Default is false.</param>
        /// <returns>The computed y values for each x.</returns>
        public double[] EvalSlope(double[] x, bool debug = false)
        {
            CheckAlreadyFitted();

            int n = x.Length;
            double[] qPrime = new double[n];
            _lastIndex = 0; // Reset simultaneous traversal in case there are multiple calls

            for (int i = 0; i < n; i++)
            {
                // Find which spline can be used to compute this x (by simultaneous traverse)
                int j = GetNextXIndex(x[i]);

                // Evaluate using j'th spline
                double dx = xOrig[j + 1] - xOrig[j];
                double dy = yOrig[j + 1] - yOrig[j];
                double t = (x[i] - xOrig[j]) / dx;

                // From equation 5 we could also compute q' (qp) which is the slope at this x
                qPrime[i] = dy / dx
                    + (1 - 2 * t) * (a[j] * (1 - t) + b[j] * t) / dx
                    + t * (1 - t) * (b[j] - a[j]) / dx;

                if (debug) Console.WriteLine("[{0}]: xs = {1}, j = {2}, t = {3}", i, x[i], j, t);
            }

            return qPrime;
        }

        #endregion

        #region Static Methods

        /// <summary>
        /// Static all-in-one method to fit the splines and evaluate at X coordinates.
        /// </summary>
        /// <param name="x">Input. X coordinates to fit.</param>
        /// <param name="y">Input. Y coordinates to fit.</param>
        /// <param name="xs">Input. X coordinates to evaluate the fitted curve at.</param>
        /// <param name="startSlope">Optional slope constraint for the first point. Single.NaN means no constraint.</param>
        /// <param name="endSlope">Optional slope constraint for the final point. Single.NaN means no constraint.</param>
        /// <param name="debug">Turn on console output. Default is false.</param>
        /// <returns>The computed y values for each xs.</returns>
        public static double[] Compute(double[] x, double[] y, double[] xs, double startSlope = double.NaN, double endSlope = double.NaN, bool debug = false)
        {
            CubicSpline spline = new CubicSpline();
            return spline.FitAndEval(x, y, xs, startSlope, endSlope, debug);
        }

        /// <summary>
        /// Fit the input x,y points using a 'geometric' strategy so that y does not have to be a single-valued
        /// function of x.
        /// </summary>
        /// <param name="x">Input x coordinates.</param>
        /// <param name="y">Input y coordinates, do not need to be a single-valued function of x.</param>
        /// <param name="nOutputPoints">How many output points to create.</param>
        /// <param name="xs">Output (interpolated) x values.</param>
        /// <param name="ys">Output (interpolated) y values.</param>
        public static void FitGeometric(double[] x, double[] y, int nOutputPoints, out double[] xs, out double[] ys)
        {
            // Compute distances
            int n = x.Length;
            double[] dists = new double[n]; // cumulative distance
            dists[0] = 0;
            double totalDist = 0;

            for (int i = 1; i < n; i++)
            {
                double dx = x[i] - x[i - 1];
                double dy = y[i] - y[i - 1];
                double dist = (double)Math.Sqrt(dx * dx + dy * dy);
                totalDist += dist;
                dists[i] = totalDist;
            }

            // Create 'times' to interpolate to
            double dt = totalDist / (nOutputPoints - 1);
            double[] times = new double[nOutputPoints];
            times[0] = 0;

            for (int i = 1; i < nOutputPoints; i++)
            {
                times[i] = times[i - 1] + dt;
            }

            // Spline fit both x and y to times
            CubicSpline xSpline = new CubicSpline();
            xs = xSpline.FitAndEval(dists, x, times);

            CubicSpline ySpline = new CubicSpline();
            ys = ySpline.FitAndEval(dists, y, times);
        }

        #endregion
    }
}

// TriDiagonalMatrix.cs

// *************************************************************************************
// SCICHART® Copyright SciChart Ltd. 2011-2018. All rights reserved.
//  
// Web: http://www.scichart.com
//   Support: support@scichart.com
//   Sales:   sales@scichart.com
// 
// TriDiagonalMatrix.cs is part of the SCICHART® Examples. Permission is hereby granted
// to modify, create derivative works, distribute and publish any part of this source
// code whether for commercial, private or personal use. 
// 
// The SCICHART® examples are distributed in the hope that they will be useful, but
// without any warranty. It is provided "AS IS" without warranty of any kind, either
// expressed or implied. 
// *************************************************************************************
using System;
using System.Diagnostics;
using System.Text;

namespace SciChart.Examples.Examples.CreateACustomChart.SplineLineSeries
{
    /// <summary>
    /// A tri-diagonal matrix has non-zero entries only on the main diagonal, the diagonal above the main (super), and the
    /// diagonal below the main (sub).
    /// </summary>
    /// <remarks>
    /// <para>
    /// This is based on the wikipedia article: http://en.wikipedia.org/wiki/Tridiagonal_matrix_algorithm
    /// </para>
    /// <para>
    /// The entries in the matrix on a particular row are A[i], B[i], and C[i] where i is the row index.
    /// B is the main diagonal, and so for an NxN matrix B is length N and all elements are used.
    /// So for row 0, the first two values are B[0] and C[0].
    /// And for row N-1, the last two values are A[N-1] and B[N-1].
    /// That means that A[0] is not actually on the matrix and is therefore never used, and same with C[N-1].
    /// </para>
    /// </remarks>
    public class TriDiagonalMatrixF
    {
        /// <summary>
        /// The values for the sub-diagonal. A[0] is never used.
        /// </summary>
        public double[] A;

        /// <summary>
        /// The values for the main diagonal.
        /// </summary>
        public double[] B;

        /// <summary>
        /// The values for the super-diagonal. C[C.Length-1] is never used.
        /// </summary>
        public double[] C;

        /// <summary>
        /// The width and height of this matrix.
        /// </summary>
        public int N
        {
            get { return (A != null ? A.Length : 0); }
        }

        /// <summary>
        /// Indexer. Setter throws an exception if you try to set any not on the super, main, or sub diagonals.
        /// </summary>
        public double this[int row, int col]
        {
            get
            {
                int di = row - col;

                if (di == 0)
                {
                    return B[row];
                }
                else if (di == -1)
                {
                    Debug.Assert(row < N - 1);
                    return C[row];
                }
                else if (di == 1)
                {
                    Debug.Assert(row > 0);
                    return A[row];
                }
                else return 0;
            }
            set
            {
                int di = row - col;

                if (di == 0)
                {
                    B[row] = value;
                }
                else if (di == -1)
                {
                    Debug.Assert(row < N - 1);
                    C[row] = value;
                }
                else if (di == 1)
                {
                    Debug.Assert(row > 0);
                    A[row] = value;
                }
                else
                {
                    throw new ArgumentException("Only the main, super, and sub diagonals can be set.");
                }
            }
        }

        /// <summary>
        /// Construct an NxN matrix.
        /// </summary>
        public TriDiagonalMatrixF(int n)
        {
            this.A = new double[n];
            this.B = new double[n];
            this.C = new double[n];
        }

        /// <summary>
        /// Produce a string representation of the contents of this matrix.
        /// </summary>
        /// <param name="fmt">Optional. For String.Format. Must include the colon. Examples are ':0.000' and ',5:0.00' </param>
        /// <param name="prefix">Optional. Per-line indentation prefix.</param>
        public string ToDisplayString(string fmt = "", string prefix = "")
        {
            if (this.N > 0)
            {
                var s = new StringBuilder();
                string formatString = "{0" + fmt + "}";

                for (int r = 0; r < N; r++)
                {
                    s.Append(prefix);

                    for (int c = 0; c < N; c++)
                    {
                        s.AppendFormat(formatString, this[r, c]);
                        if (c < N - 1) s.Append(", ");
                    }

                    s.AppendLine();
                }

                return s.ToString();
            }
            else
            {
                return prefix + "0x0 Matrix";
            }
        }

        /// <summary>
        /// Solve the system of equations this*x=d given the specified d.
        /// </summary>
        /// <remarks>
        /// Uses the Thomas algorithm described in the wikipedia article: http://en.wikipedia.org/wiki/Tridiagonal_matrix_algorithm
        /// Not optimized. Not destructive.
        /// </remarks>
        /// <param name="d">Right side of the equation.</param>
        public double[] Solve(double[] d)
        {
            int n = this.N;

            if (d.Length != n)
            {
                throw new ArgumentException("The input d is not the same size as this matrix.");
            }

            // cPrime
            double[] cPrime = new double[n];
            cPrime[0] = C[0] / B[0];

            for (int i = 1; i < n; i++)
            {
                cPrime[i] = C[i] / (B[i] - cPrime[i - 1] * A[i]);
            }

            // dPrime
            double[] dPrime = new double[n];
            dPrime[0] = d[0] / B[0];

            for (int i = 1; i < n; i++)
            {
                dPrime[i] = (d[i] - dPrime[i - 1] * A[i]) / (B[i] - cPrime[i - 1] * A[i]);
            }

            // Back substitution
            double[] x = new double[n];
            x[n - 1] = dPrime[n - 1];

            for (int i = n - 2; i >= 0; i--)
            {
                x[i] = dPrime[i] - cPrime[i] * x[i + 1];
            }

            return x;
        }
    }
}

< BACK TO ALL WPF CHART CHART EXAMPLES